Las mezclas triaxiales de vidriados son una manera bastante eficaz de obtener nuevos vidriados a partir de otros conocidos. El método consiste en elegir tres vidriados de partida, de los cuales se obtienen otros a partir de las mezclas en distintas proporciones de dicho trío de vidriados. En general, el método se suele aplicar de dos formas diferentes. En una de ellas, los tres vidriados de partida tienen la misma base y solo varían en los colorantes que se añaden. De esta manera, pueden obtenerse gamas de mezclas de colores. La otra posibilidad es utilizar tres vidriados de cualquier tipo o incluso materias primas individuales para hacer las mezclas. Si seguimos este método, obtendremos más resultados útiles si los tres vidriados de partida ya dan por si mismos buenos resultados.
Este tipo de mezclas se entiende muy bien a partir de los diagramas traxiales que describen las proporciones de todas las mezclas que se obtienen. Por ejemplo, en la figura siguiente se muestran mezclas de color en una base común. Como todos los vidriados tienen la misma base, no es necesario incluir la receta de dicha base para los cálculos, sino que basta solo con los colorantes.
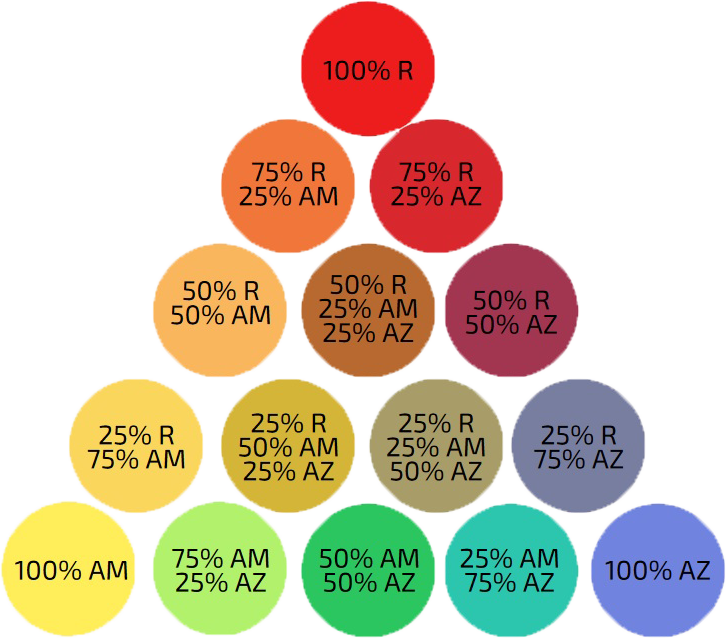
Los vidriados en los vértices del triángulo tienen un 100% de rojo (arriba), 100% de azul (abajo-derecha) y 100% de amarillo (abajo-izquierda). El resto de vidriados tiene una composición proporcional a la distancia a la que se encuentra dicho vidriado de cada esquina, y esa proporción depende del número de muestras que hay en cada lado del triángulo. Por ejemplo, la segunda muestra, si nos movemos de arriba a abajo y de izquierda a derecha, tiene 75% de rojo y 25% de amarillo. Eso es porque se encuentra a un salto de distancia al rojo y a tres saltos hacia el amarillo. En total hay cuatro saltos en la fila entre el rojo y el amarillo, por eso cada salto es del 25%, ya que 100/4=25. Es casi más fácil de pensar que de leer.
Pero, ¿cómo hago la cuenta cuando un vidriado no está sobre los lados del triángulo? Ahora, igual que antes, se hace contando saltos. Por ejemplo, con el mismo orden de antes, vamos a calcular la proporción de cada colorante para el vidriado n° 5. Está a 2 saltos del rojo, luego tiene un 100 - 25*2 = 50% de rojo. Del azul está a 3 saltos (para ver claro cada salto tenemos que ir desde el azul por la perpendicular a la línea amarillo-rojo hacia esta línea, que es lo mismo que hemos hecho en el rojo, pero en ese caso la perpendicular a la línea amarillo-azul coincidía con la vertical), así que 100 - 25*3 = 25%. Para el amarillo también hay tres saltos, luego tambien un 25% de colorante amarillo.
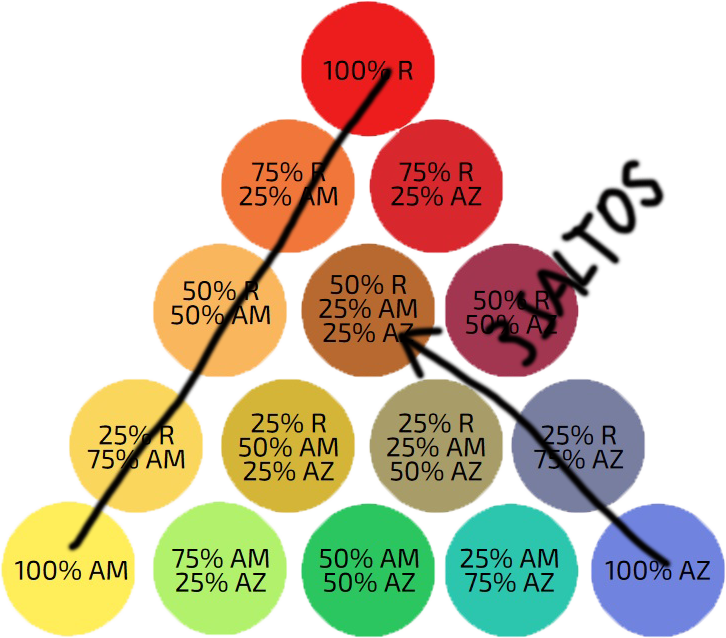
Este método suele emplearse para hacer 15 mezclas, como en el ejemplo descrito, o 10. En este caso, el lado del triángulo tendría tres saltos, por lo que cada salto sería del 33,3% (100/3 = 33,3). Y, si hiciésemos un muestrario más grande, de 21 muestras, cada lado tendría 5 saltos por lo que cada salto sería del 20%.
En la siguiente imagen vemos una mezcla de 21 muestras con tres vidriados en los vértices que tienen diferentes recetas. El vértice superior del triángulo representa 100% pasta PF; el vértice inferior izquierdo, 100% de ortosa y el vértice inferior derecho 30% pasta PF, 30% ortosa y 40% dolomita.

Como ejemplo, voy a calcular la composición del vidriado n° 9, que está a la derecha de uno muy oscuro en el que se lee un 8. Solo hay que contar los saltos a cada vértice y hacer las cuentas. En este caso, cada salto representa un 20%. Desde el vértice superior hay 3 saltos, lo cual significa que ponemos un 40% de la composición de ese vidriado (100 - 20*3 = 40). Desde el vértice inferior derecho hay 4 saltos (se pone un 20%), y desde el vértice inferior derecho hay 3 saltos, así que otro 40%. Entonces, la composición del vidriado n° 9 es: 40% de la receta del vidriado del vertice superior, 20% de la receta del vidriado del vértice inferior izquierdo, y 40% de la receta del vidriado del vértice inferior derecho.
Se pueden calcular porcentajes muy rápido simplemente multiplicando. Por ejemplo, para calcular el 40% de algo, simplemente multiplico por 0,4. Teniendo esto en cuenta, los cálculos son: 100*0,4=40% de pasta PF (ya que la receta del vidriado del vértice superior es 100% de pasta PF). Del vértice inferior izquierdo nos sale 100*0,2=20% de ortosa. La receta del vértice inferior derecho es ligeramente más compleja, ya que tiene tres componentes, pero los cálculos son idénticos: 30*0,4=12% de pasta PF, más 30*0,4=12% de ortosa, más 40*0,4=16% de dolomita. Si ahora lo sumamos todo, la receta del vidriado n° 9 es: 52% de pasta PF, 32% de ortosa y 16% de dolomita.
Finalmente, decir que para sacar las 21 muestras de la foto no es necesario calcular la receta de cada uno de los vidriados. Solo necesitamos saber las recetas de los vidriados de los vértices, y para preparar el resto de vidriados haremos mezclas proporcionales de volúmenes de estos tres vidriados. Este es un método que nos evita pesar muchos vidriados de forma independiente, y suele conocerse como "método de mezclas volumétricas", pero eso se explica en otro lugar.